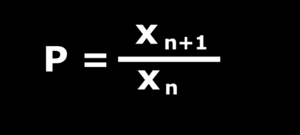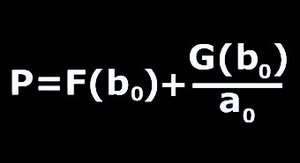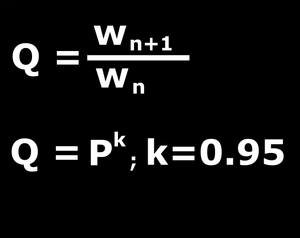Skálatörvények
A Liesegang mintázatok közös sajátsága, hogy valamennyien mutatnak olyan térbeli és időbeli szabályosságokat, amelyek matematikailag is leírhatók. Ezeket az egyszerű összefüggéseket nevezzük skálatörvényeknek, amelyekből a Liesegang mintázatok esetén összesen négy van.

A távolságtörvény
Az első matematikai szabályosság az úgynevezett távolságtörvény, amit 1923-ban Jablczinsky írt le elsőként. Legyen xn a gél felszínétől számított n-edik csapadéksáv távolsága az elektrolitok érintkezési pontjától. Jablczinsky azt vette észre, hogy a szomszédos zónák távolságainak hányadosa (xn+1/xn) egy mintázaton belül állandó, vagyis azok mértani sorozatot alkotnak. Ennek a sorozatnak a kvóciense – amit gyakran „távolsági koefficiens” néven említenek – általában 1-nél nagyobb szám, de a valós kísérletekben a 1,5-es értéket csak ritkán haladja meg.
Bár a távolságtörvény eredete els látásra egyáltalán nem nyilvánvaló, Ostwald eredeti túltelítési modellje alapján matematikai egzaktsággal megindokolható. 1955-ben Carl Wagner megmutatta, hogy ha feltételezzük a csapadéksávok létezését, akkor azoknak szükségszerűen a távolságtörvény szerint kell elhelyezkedniük.
Szabályos és fordított mintázatok
Léteznek olyan anomális mintázatok, amelyeknél a távolsági koefficiens értéke 1-nél kisebb szám. Ezeket „fordított” mintázatoknak hívjuk, hiszen bennük a zónák távolságai a diffúzió irányba haladva csökkennek, vagyis a mintázat egész véve úgy néz ki, mintha egy normál rendszert a feje tetejére állítottunk volna.
A fordított mintázatokkal kapcsolatban a legnagyobb elméleti probléma az volt, hogy Wagner fent említett elmélete értelmében nem is létezhetnének. És mégis itt vannak...

Az időtörvény
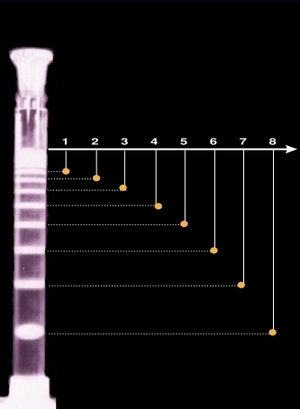
Jelölje tn az n. csapadéksáv keletkezéséig eltelt időt. A Liesegang mintázatokra általában igaz, hogy az xn2/tn hányados n növekedtével egy adott értékhez tart. Ez az egyszerű szabályosság, amit először Morse és Pierce írt le a jelenség diffúziólimitált jellegéből következik. Ugyanakkor az már nem nyilvánvaló, hogy ennek autokatalitikus reakció esetében is így kell lennie, mivel egy ilyen folyamat sebessége az időnek nem monoton függvénye.
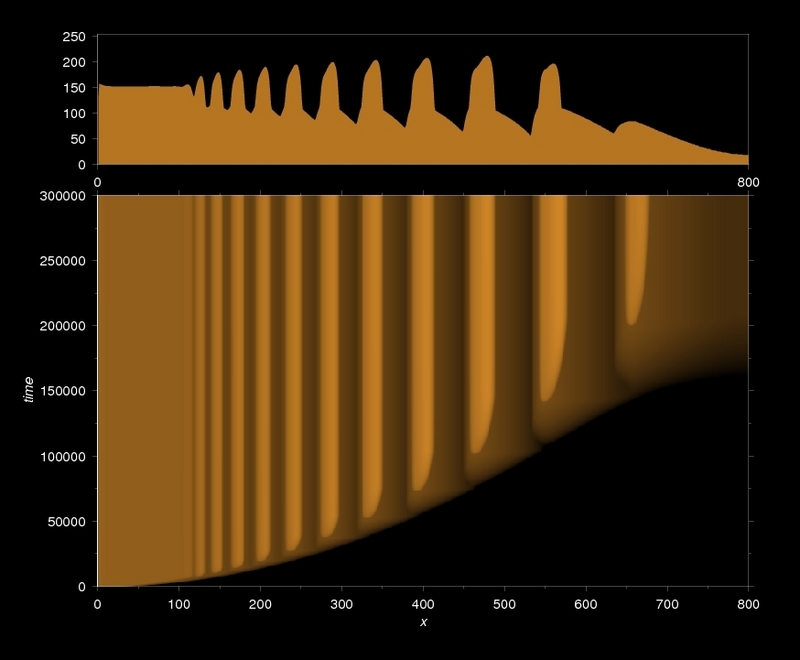
Az időtörvény: a Liesegang mintázatok képződése diffúzió által limitált kinetika szerint zajlik (a képen egy az IDNB modell alapján szimulált 1D mintázat tér-idő diagramja látható)

A Matalon-Packter szabály
A Liesegang-jelenséggel kapcsolatos kísérletek középpontjában általában a távolságtörvény. E kísérletek tanúsága szerint a távolsági koefficiens nem egy univerzális állandó, hanem kísérletileg kontrollálható és belső (rejtett) paraméterektől egyaránt függ. (Az utóbbira bizonyos elméleti megfontolások illetve kísérletileg megfigyelhető ellentmondások is utalnak.)
A távolsági koefficiensnek a két elektrolit koncentrációjától való függését elsőként Matalon és Packter tanulmányozták. Kísérleti tapasztalataik szerint a távolsági koefficiens (P) fordítottan arányos a külső elektrolit koncentrációjával (1/a0). E függvénynek mind a meredeksége, mind a tengelymetszete csökkenő függvénye a belső elektrolit koncentrációjának (b0).

A szélességtörvény
A Liesegang mintázatok úgynevezett szélességtörvényének létezik egy gyengébb és egy erősebb megfogalmazása. Az IDNB modell alapján végzett tömeges 1D szimulációk alapján a gyengébb forma érvényesnek bizonyult, míg az erősebb forma csupán jó közelítésnek tekinthető. Utóbbi valójában ízlés dolga: az erősebb formát nevezhetjük teljes (ámbár elegáns) tévedésnek is (lásd a tömeges szimulációkról szóló menüpontot).
A gyengébb megfogalmazás szerint ha wn jelöli az n. csapadékzóna vastagságát, akkor a wn+1/wn hányados ugyanúgy konstans, mint a távolságok hányadosa, vagyis a zónaszélességek szintén mértani sorozatot alkotnak.
Az erősebb állítás szerint ha P a távolsági koefficiens, Q pedig a szélességek mértani sorozatának kvóciense, akkor utóbbi minden esetben kifejezhető, mint az előbbi hatványa, sőt, egyes szerzők mind kísérleti, mind elméleti megfontolások alapján odáig merészkedtek, hogy a hatványkitevő univerzális állandó, melynek értéke valahol 0,9 és 0,95 között lehet.