A mintázatkettőződési (double banding) effektus
Mintázatkettőződésről akkor beszélünk, ha egy Liesegang struktúra kétféle periodicitást mutat egyszerre. Ezek a mintázatok nagyjából úgy néznek ki, mintha két Liesegang rendszert egymásba toltunk volna. Valószínűleg ez az oka annak, hogy a kutatók többsége a jelenséget olyan szennyeződéseknek tulajdonította, amelyek maguk is mintázatot képeznek.
R. F. Sultan néhány éve kísérletileg bebizonyította, hogy a Liesegang rendszerek efféle kombinálása valóban lehetséges: ha egy gél két olyan vegyületet tartalmaz, amelyek csapadékot tudnak képezni a külső elektrolittal, akkor valóban a két tiszta mintázat valamiféle kombinációját kapjuk, ami azonban nem igazán hasonlít a mintázatkettőződési effektusra.
Az IDNB modell segítségével belátható volt, hogy a többszörös periodicitás valóban egyetlen anyaggal is kiváltható. A szimulációk tanúsága szerint a mintázatkettőződésnek nagyjából három altípusa különböztethető meg. Léteznek alternáló (bifurkációs) mintázatok, van klasszikus kettőződés (double banding) illetve valójában ide tartoznak a kaotikus mintázatok is. A három típus között folytonos az átmenet, az egy adott típushoz tartozó vektorok pedig összefüggő részt foglalnak el a paramétertérben.
Alternáló mintázatok (bifurkáció)
Ha egy normál mintázat paramétereivel megközelítjük azt a tartományt, ahol a klasszikus kettőződés megjelenik, előbb olyan alternáló mintázatokat látunk, amelyekben váltakoznak a vékony és vastag csapadékzónák. A szimulációk alapján úgy tűnik, hogy a klasszikus mintázatkettőződéshez tartozó paraméterpontok tartományát minden irányból héjként veszik körbe azok a pontok, amelyeknél csupán bifurkáció lép fel.
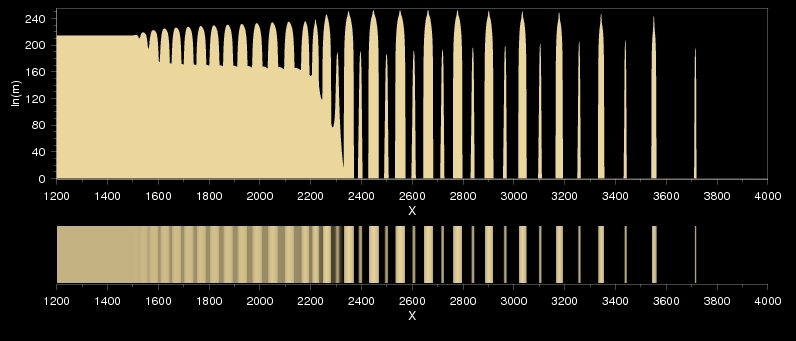
Váltakozva megjelenő vékony és vastag csapadékzónák: a mintázatkettőződés (double banding) egy speciális esete.
Klasszikus mintázatkettőződés
A megfelelő paramétertartományban az alábbihoz hasonló mintázatokat látunk. Ez a kettőzött mintázatok irodalomban leírt klasszikus formája: egy normál mintázat csapadékzónái között jóval sűrűbben elhelyezkedő keskeny zónák figyelhetők meg.
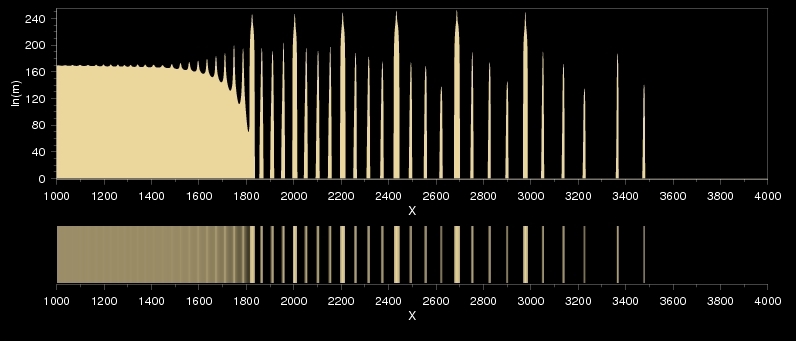
A mintázatkettőződés klasszikus formája: két különböző frekvencia figyelhető meg egyetlen rendszeren belül úgy, hogy az csupán egyféle csapadékot tartalmaz.
Kaotikus viselkedés
Valahol a fenti két mintázatképződési formának megfelelő régiók határán található egy olyan paramétertartomány, amelyben szabálytalan mintázatok képződnek. Az ilyen rendszerekben is megkülönböztethetünk elsődleges és másodlagos zónákat, de ezek elhelyezkedésében sem együtt, sem külön-külön nem látható semmiféle szabályosság, a mintázat kaotikus. (A "kaotikus" kifejezés itt csupán a formára utal, tehát nem a fizikában szokásos dinamikai értelemben jellemzi a rendszert!)
Fontos megjegyezni, hogy az ilyen mintázatokat eredményező 1D modell nem tartalmaz semmiféle sztochasztikus elemet, a szabálytalanság tehát nem ebből, hanem a determinisztikus modell matematikai viselkedéséből ered.
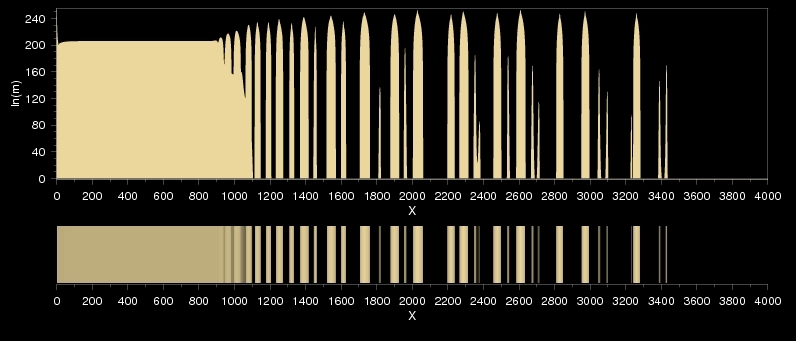
Mintázat rend nélkül: elsőre meglepő ugyan, de ez az effektus nem egyéb, mint a mintázatkettőződés egy speciális esete.