Tömeges szimulációk
Analitikus megoldási módszerek hiányában nagy tömegben végrehajtott 1D szimulációk segítségével ellenőrizhető, hogy egy adott modell, esetünkben Ostwald eredeti túltelítési elmélete, illetve az IDNB modell egy egyszerűsített változata valóban minden fizikailag szóba jöhető paraméteregyüttes mellett megfelelően teljesít-e.

A túltelítési modell mint közös alap
A Liesegang-jelenség átfogó modelljének fejlesztésénél először nyilván célszerű volt azon elgondolkodni, hogy a létező elképzelések mely részei emelhetők át bele. Ostwald túltelítési elmélete régi és egyben túlegyszerűsített is, ugyanakkor megvan az a kétségtelen előnye, hogy a Liesegang mintázatok alapvető skálatörvényeit helyesen adja vissza. Ezt a tömeges szimulációk eredménye is alátámasztotta.
Wilhelm Ostwald 1897-es elképzelése ráadásul egy közismert jelenségre alapoz, ami szintén előny. Túltelített, metastabil oldat valóban számos anyagból készíthető, ez a stabilitás pedig pillanatszerűen szűnik meg, ha az oldatot egy kristályszemcsével hozzuk érintkezésbe. Ezt a módszert „beoltásnak” nevezik és a gyakorlatban is előszeretettel alkalmazzák olyan anyagok előállítása során, amelyeknél a kristályosodás kinetikailag gátolt.
Ostwald elmélete szerint tehát a periodikus csapadékleválás nem egyéb, mint térben és időben ismétlődő „önbeoltás”. Bár ez a magyarázat így elsőre teljesen logikusnak tűnik, azért van vele néhány probléma. Ha például megpróbálunk Liesegang-mintázatokat szimulálni a túltelítési elmélet alapján felírható egyenletekre alapozva, hamar kiderül, hogy a valós kísérletekkel szemben itt szinte végtelenül keskeny csapadékzónákat kapunk.
Mindezzel együtt a túltelítési modell jó alapul szolgált az IDNB modellhez.
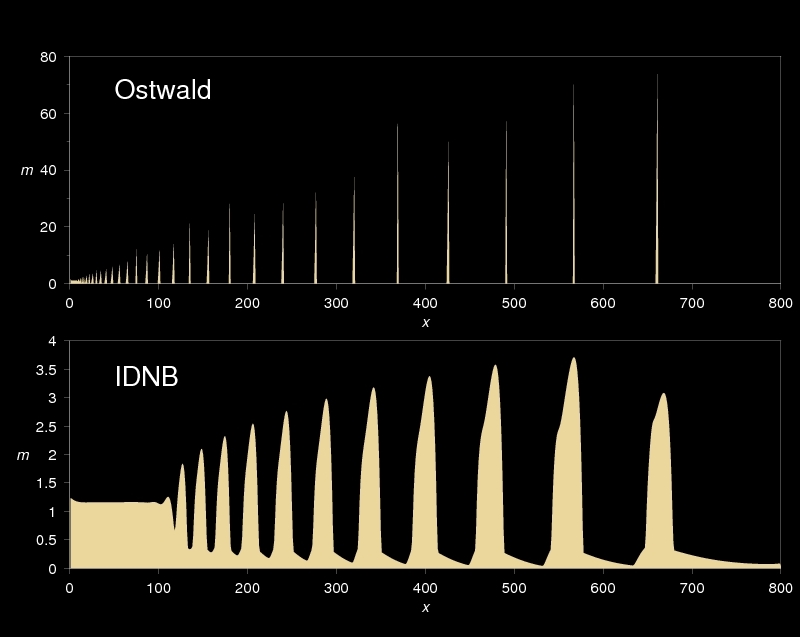
Ostwlad eredeti modellje, illetve a megfelelő kiegészítésekkel ellátott általános modell által eredményezett 1D mintázat

Tömeges szimulációk - a módszer
Az IDNB modell átfogó érvényességének ellenőrzése végett két sorozatban hajtottam végre nagy tömegű 1D szimulációkat.
Az első sorozatban az eredeti túltelítési modellt használtam, és előállítottam a megfelelő 1D mintázatot a a paramétertér egy kémiailag plauzibilis tartományában, körülbelül 40.000 pontban. A második sorozatban az IDNB modell egy egyszerűsített változatát használtam ugyanígy.
Bár egy vagy néhány 1D Liesegang mintázat „kézi” kiértékelése (a jellemző paraméterek meghatározása) nem különösebben bonyolult dolog, ugyanezt több tízezer mintázattal elvégezni már nem triviális feladat. Szintén célszerűtlen a szimulációt ténylegesen végrehajtani a paramétertér minden rácspontjában, hiszen a tapasztalatok szerint a pontok körülbelül 60%-a olyan paraméteregyüttesnek felel meg, ami semmiféle mintázatot nem eredményez. Ha ezeket nem szűrjük ki, az akár több hónappal hosszabbíthatja meg a szükséges futásidőt! Ennek megfelelően az első feladat egy olyan trükkös „mesterséges intelligencia” megírása volt, ami tartalmazott egy „mintázatdetektort” és ennek segítségével képes volt kellően nagy valószínűséggel megjósolni, hogy a parmétertér egy-egy pontjához tartozik-e Liesegang mintázat, vagyis érdemes-e egyáltalán elindítani a számolást.
Ha van egy ilyen „csodafegyverünk” a feladat már csak annak a 6-8 dimenziós hiperkockának a kijelölése a paramétertérben, amelynek határai körülbelül megfelelnek a valós kísérletek viszonyainak. Mivel a szomszédos rácspontokban végrehajtott szimulációk egymástól gyakorlatilag függetlenek, a pásztázás folyamata kiválóan párhuzamosítható, a részfeladatok pedig optimálisan szétoszthatók akár egy heterogén klaszter csomópontjain is.

Eredmények
Bár a valós kísérletekben a távolsági koefficiens értéke ritkán haladja meg a 1,5-et, tisztán matematikai szempontból a túltelítési elmélet ennél sokkal ritkásabb mintázatokat is eredményezhet. Ennek az ellentmondásnak az egyik legvalószínűbb oka az a tény, hogy a szimulációt nyilván nem gátolják bizonyos fizikai korlátok. A szimulációkban például szabadon választhatjuk meg a kritikus túltelítés mértékét vagy diffúzióállandók arányát, miközben a való életben ezeket gyakorlatilag nem tudjuk befolyásolni. Szimulációval tehát olyan mintázatokat is elő tudunk állítani, amelyek fizikailag plauzibilisek ugyan, de a nekik megfelelő paraméteregyüttes egyetlen valós rendszernek sem feleltethető meg. A másik ok a túltelítési modell által nyújtott túlegyszerűsített leírás. Ez utóbbi már csak azért is valószínű, mert az IDNB modellel végzett szimulációk gyakorlatilag nem mutattak ilyen eltérést.
A kiértékelés után keletkezett eredmények illesztését ortogonális polinomokkal lehet elvégezni. Az Ostwald modell esetében ebből az 1,5-nél nagyobb távolsági koefficienssel rendelkező mintázatok az elmondottak miatt kimaradtak.
Az alapvető skálatörvények a paramétertér egészén érvényesnek bizonyultak. (Az Ostwald modellnél a szélességtörvényt nyilván nem lehetett ellenőrizni.) Az is kiderült, hogy a mintázatképződéshez vezető paraméteregyüttesek (paramétervektorok) a hipertérben egyetlen folytonos testet alkotnak. Nincsenek tehát a mintázatképző tartományban lyukak, vagy elzárt szigetek.
Az illesztett függvényekből két további érdekes következtetést lehetett levonni. A kísérletileg (gyakorlatilag heurisztikusan) felfedezett Matalon-Packter szabály érvényes ugyan, de az illesztett polinomok összetétele alapján valójában inkább csak jó közelítés, semmint a modellből következő matematikai szabályosság.
Hasonlóan érdekes eredményre vezetett a szélességtörvény vizsgálata.

A szélességtörvény érvényességéről
A szélességtörvény gyengébb formája (a szomszédos zónák szélességének hányadosa állandó) a teljes paramétertérben érvényesnek bizonyult.
Ami az erősebb formát illeti, az gyakorlatilag azt állítja, hogy egzakt matematikai összefüggés áll fenn a távolsági koefficiens és a zónaszélességek sorozatának kvóciense között.
A tömeges szimulációk értékelése ugyanakkor azt mutatja, hogy bár ez a két skálatörvény valóban erős hasonlóságot mutat, közvetlen matematikai kapcsolat köztük nincsen.
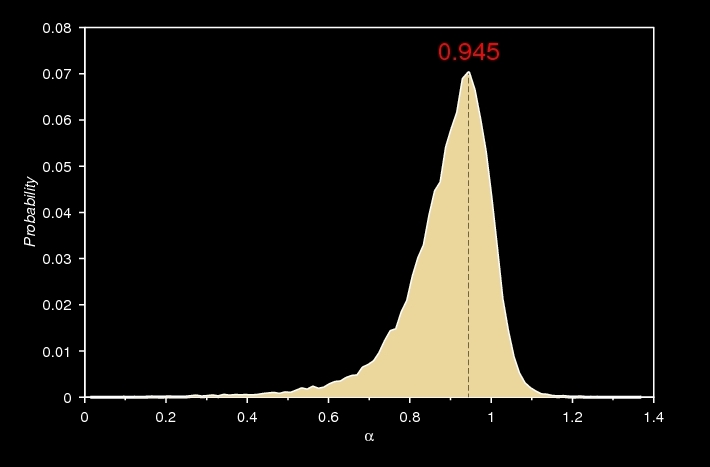
A zónák vastagságának távolságtól való függése valójában nem írható le egy egyszerű hatványfüggvénnyel, amint azt korábban többen javasolták, mivel a kérdéses összefüggés exponense a szimulációkban nem bizonyult univerzálisan állandónak. Az ugyanakkor igaz, hogy az exponens gyakorisági eloszlása egy meglehetősen keskeny csúcsot eredményez 1 körül, a csúcspont pedig az a bizonyos 0,95-ös érték, amit más szerzők univerzálisnak gondoltak. Statisztikailag tehát egyáltalán nem meglepő, hogy a valós kísérletek alapján egyesek erre a téves következtetésre jutottak.