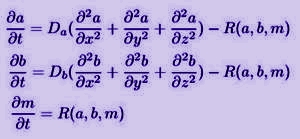Alapötlet

A Liesegang-jelenség első elméletét 1897-ben publikálta Wilhelm Ostwald saját, általános kémiáról szóló könyvében. A kémiában közismert, hogy egyes anyagok kristályosodása csak túltelített oldatból indul meg, mivel a nukleációs gócok képződése kinetikailag gátolt. Ez a kísérleti tapasztalat jelentette Ostwald „túltelítési elméletének” alapját.

E szerint az elképzelés szerint a két elektrolit rendszere túltelített marad az első kristály képződéséig. Ezen a ponton aztán robbanásszerűen megindul a szilárd anyag képződése, hiszen az első kristálygóc környezet ekkorra már kellően messze van az egyensúlyi állapottól. Mindez azt jelenti, hogy a kémia reakció egy időre annyira begyorsul, hogy azt a lassú diffúzió nem képes táplálni, vagyis a reakciózóna két oldalán egy-egy széles kiürített sáv keletkezik. A mintázatképződés során tulajdonképpen ez az eseménysor ismétlődik meg sokszor, az okozza a rendszer térbeli és időbeli periodicitását.

Eredmények

Több mint száz éves kora ellenére a szó bizonyos értelmében a túltelítési elmélet a Liesegang-jelenség egyik llegsikeresebb modellje. Egyaránt képes magyarázatot adni a távolság és az időtörvényre bár ezt matematikailag csak 1952-ben mutatták meg.

Ugyanakkor az is bizonyítható vele kapcsolatban, hogy nem egyeztethető össze a fordított mintázatok keletkezésével, illetve más, nyilvánvalóan létező és reprodukálható anomáliákkal. Szintén elvi problémát jelent vele kapcsolatban, hogy matematikai struktúrájából adódóan végtelenül keskeny csapadéksávokat jósol, ami nem realisztikus, illetve szintén kizárja a távolságtörvény indokolhatóságát.

Alapötlet

A szolkoagulációs elmélet alapfeltevése szerint a csapadék először híg, stabil kolloid diszperzió (szol) formájában keletkezik. A látható csapadék úgy jön létre, hogy a külső elektrolit fölöslege hatására ennek a szolnak a stabilitása megszűnik, majd kicsapódik.

Eredmények

Az elmélet gyenge pontja nem is a csapadéksávok, hanem a köztük levő üres zónák képződésének magyarázata. A modell szerint a kezdetben képződő szol részecskéi annyira kicsik, hogy szabadon diffundálhatnak a gélmátrixban, így képes a koncentrációjuk a kicsapódott régiók környezetében lecsökkenni. Erre a feltevésre ugyanakkor semmiféle kísérleti bizonyíték nincs. A szolrészecskék tömege nyilván sokkal nagyobb kell legyen, mint az ionoké, vagyis mozgásuk nagyságrendekkel lassúbb, már ha egyáltalán képesek jelentős mértékben mozogni. Márpedig ilyen lassú mozgással egészen biztosan nem alakíthatnak ki akkora üres zónákat, amelyek a kísérletekben megfigyelhetők (Valós kísérletekben néhol 1-2 cm széles csapadéksávok és 30-40 cm-es üres régiók jelennek meg!)

Alapötlet

A szolkoagulációs modellel kapcsolatban említett elvi problémák kiküszöbölésére számos szerző olyan modelleket javasolt, amelyek lényege, hogy a két elektrolit kezdetben molekulákat, vagy nagyon kis részecskéket képez. Ezek a köztitermék-részecskék szabadon diffundálhatnak a rendszerben ugyanolyan sebességgel, mint az ionok, majd ha koncentrációjuk elér egy kritikus küszöböt, akkor látható csapadékot képeznek. Az erre az alapötletre felépített elméletek lényegében csak a csapadékképződés kinetikájában térnek el egymástól.

Eredmnyek

A diffuzív intermedierek létezésére jelenleg semmiféle kísérleti bizonyíték nincs.

Ezzel együtt az ebbe a csoportba tartozó modellek részben sikeresek, ami azt jelenti, hogy képesek reprodukálni a mintázatok kváziperiodikus jellegét, a távolság- és az időtörvényt, sőt, még a Matalon-Packter törvény is levezethető ebből az alapfeltevésből kiindulva. Ugyanakkor a morfológia anomáliákkal kapcsolatban ezek a modellek semmilyen eredményre nem vezettek.

Alapötlet

Bizonyos kísérleti eredmények arra utalnak, hogy csapadékmintázatok külső koncentrációgradiens nélkül is képződhetnek. Egy olyan zselatin gélben például, amely kezdetben egyenletesen eloszlatott ólom-jodid szolt tartalmaz spontán módon mintázat képződhet egyfajta durvulási mechanizmussal.

A kompetitív részecskenövekedési modell szerint a mintázatképződés hajtóereje az a termodinamikai instabilitás (Lifshitz-Slyozov instabilitás), ami a szolrészecskék méretbeli inhomogenitásából ered. A kisebb átmérőjű részecskéknek nagyobb a felületi feszültsége, ami oldhatóságuk enyhe növekedését okozza a nagyobbakéhoz képest. Ez pedig azt jelenti, hogy egy ilyen rendszerben a nagyobb részekék a kisebbek rovására képesek növekedni, míg utóbbiak végül teljesen eltűnnek a rendszerből, üres régiókat hagyva maguk után. A csapadékzónákat a nagyobb részecskék alkotják.

Eredmények

Polezhaev és Müller sikeresen alkalmazta ennek az elképzelésnek és a túltelítési elméletnek egy kombinációját a szabályos Liesegang mintázatok leírására. Modelljükben ugyanakkor ők is kénytelenek voltak feltételezni egy diffúzióra képes intermedier létezését, a részecskék méreteloszlását tekintve pedig csak két frakciót („kicsi” és „nagy”) különböztettek meg. Ezzel együtt ez a modell felfedezése óta talán a legsikeresebb leírása a periodikus csapadékképződésnek. Numerikus szimulációk szerint 1 és 2 dimenzióban egyaránt jól teljesít, sőt, egyes morfológiai anomáliákra is képes magyarázattal szolgálni.

Később Krug és munkatársai továbbfejlesztették ezt az elképzelést: a két méret helyett teljes méreteloszlási függvényt használtak, amit egy nemlineáris részecskenövekedési modellel kombináltak.

Alapötlet

A Liesegang-jelenség történetét ismerve kijelenthető, hogy minden realisztikus eredményeket is felmutatni képes modell tartalmazott legalább egy autokatalitikus lépést. A diffúziós hullám elmélet e tekintetben kivétel, mivel autokatalízis helyett autoinhibíción alapszik. Lényege, hogy a csapadék képződését szinte minden esetben kíséri valamilyen melléktermék keletkezése. Arra is számos példát láthatunk, hogy maga a reakció visszafordítható (a csapadék feloldható) ennek az anyagnak a feleslegével. A MgCl₂ és az NH₄OH reakciójának mellékterméke például az NH₄Cl,amelynek feleslegével a keletkező Mg(OH)₂ csapadék feloldható.

A diffúziós hullám elmélet szerint a Liesegang mintázatok periodicitását a melléktermék okozza. Ahol nagy mennyiségű csapadék keletkezik, ott nyilván nagy mennyiségű melléktermék is képződik. Ez lokálisan megemeli a csapadék oldhatósági szorzatát és átmenetileg meggátolja annak további keletkezését. Az inhibíciós hatás addig marad fenn, amíg a lassú diffúzió szét nem oszlatja a melléktermék koncentrációcsúcsát.

Eredmények

Kísérleti szempontból ezzel az elmélettel kapcsolatban a legnagyobb probléma az a tény, hogy Liesegang mintázatok olyan rendszerekben is képződnek, amelyekben az említett melléktermék víz, vagy valamilyen teljesen inert anyag. Valószínűleg ez az oka annak, hogy a diffúziós hullám elméletet soha, egyetlen matematikailag egzakt leírás alapjaként sem használták. Örökre kvalitatív modell maradt.

Alapötlet

Az adszorpciós elmélet egy rendkívül egyszerű, ugyanakkor gyakorlati szempontból szinte bizonyosan kizárható magyarázattal szolgál a Liesegang mintázatok peiodicitására. Azt állítja, hogy az üres zónák azért jönnek létre, mert a keletkezett csapadék felszínén adszorbeálódik a maradék elektrolit, vagyis a csapadékzóna környezetéből elfogynak a reaktánsok.

Eredmények

Az említett adszorpciós effektus ugyan valóban létezik, ugyanakkor kizárható, hogy a csapadék képes legyen annyi elektrolitot megkötni, ami a valós rendszerekben megfigyelhető nagyságú üres zónák keletkezéséhez vezetne. Egyes rendszerekben akár fél méter (!) távolság is lehet a szomszédos zónák között.

Alapötlet

Ezt a modellt, amely tulajdonképpen a diffuzív internedieren alapuló leírások egy speciális esetének tekinthető néhány éve Rácz Zoltán javasolta. A modell értelmében a két elektrolit kezdetben egy metastabil köztiterméket hoz létre, amely a rendszerben szabadon diffundálhat. Ahol instabillá válik. Ott immár mozgásra képtelen csapadékká bomlik le.

Eredmények

Az elméletet spinek hipotetikus sokaságán numerikus szimulációkkal tesztelték, vagyis kémiai megfontolásokat tulajdonképpen nem tartalmazott. Bár a normál mintázatokra jellemző távolságtörvényt reprodukálja, viszonylag kevés kapcsolata van a valós kísérletekkel.

A normál mintázatok leírásán kívül egyéb eredményre nem vezetett.

Alapötlet

Ez a leírás alapvetően a Liesegang-jelenség egy sejtautomatán alapuló modellje, amit a közelmúltban Chopard és néhány más szerző vizsgált. A két reaktánst ebben az esetben egy-egy részecskesokaságnak tekintik, amelyek egy rácson véletlenszerű bolyongást végeznek. Ha két részecske találkozik egy rácsponton, akkor bizonyos szabályok szerint „reagálnak” egymással és immobilis fázist (csapadékot) képeznek.

Eredmények

Ez az első olyan modell, amely a véletlenek hatásával is foglalkozik. Bizonyíthatóan működik 1 és 2 dimenzióban, sikeresen reprodukálható vele a normál mintázatképződés, egy esetben pedig képes volt produkálni egy radiális mintázatban tovaterjedő hibahelyet is. (Némiképp félrevezető, hogy maguk a szerzők cikkükben ezt spirális mintaként említik, holott az ábrán ilyen nem látható, csupán egy törésszerű, tovaterjedő defektus.)

Mivel ez a modell az egyedi részecskék szintjén igyekszik megragadni a mintázatképződés lényegét, szimulációja rendkívül számításigényes.

A módszert később továbbfejlesztette Antal és munkatársai, amelynek lényege a korábban említett spinodális lebomlással való kombinálás volt. Ezzel a módosítással a modell 2 dimenzióban már semmiféle mintázatot nem eredményezett, ellenben továbbra is képes volt reprodukálni a normál mintázatot 1 és 3 dimenzióban, feltéve, hogy lineáris elrendezést alkalmaztak. Egyéb morfológiák leírására nem alkalmazták.