A "Liesegang gyűrűk" rövid története
A "Liesegang-jelenség" néven is ismert periodikus csapadékképződés története immár több mint 100 évre tekint vissza. Bár a XX. század folyamán a legkülönbözőbb terüteleteken tevékenykedő kutatók ezrei foglalkoztak a vizsgálatával, a vele kapcsolatban megjelent publikációk száma pedig hasonlóan magas, a Liesegang mintázatok keletkezésének pontos oka egészen 2003-ig tisztázatlan volt. Nem volt egyetlen olyan matematikailag egzakt, valamint kémiai és fizikai szempontból is kellően megalapozottnak mechanizmus, amely képes lett volna magyarázatot adni a Liesegang jelenségcsoporttal kapcsolatos összes effektusra és anomáliára.

Természetes mintázatok
A XX. század utolsó évtizedeiben a tudományos társadalom egyre nagyobb érdeklődést tanúsított az olyan kémiai, fizikai és bilógiai folyamatok iránt, amelyek valamiféle mintázat képzédéséhez vezetnek. A kémiai mintázatok közül a legtöbbet tanulmányozott valószínűleg az úgynevezett Belouszov-Zsabotyinszkij reakció volt, de számos vizsgálatot végeztek viszkózus ujjasodással, diffúziólimitált aggregációval, gombakolóniák és egyéb előlények morfogenezisével illetve egyes anyagok elektrokémia leválasztását kísérő mintázatképződésekkel is.
Bár a fent felsorolt rendszerek első látásra meglehetősen különbözőnek tűnnek, valójában számos hasonlóságot mutatnak mind a bennük felfedezhető mintázatok kialakulásával, mind a leírásukra alkalmazható módszerekkel kapcsolatban. Mindegyik mechanizmusban található például egy vagy több diffúzió által limitált részlépés, a mintázat kialakulása pedig minden esetben ennek, illetve a mögöttes kémiai, fizikai vagy biológiai folyamat bonyolult összjátékának eredménye.

Reakció-diffúzió rendszerek matematikai leírása
Az efféle rendszerek matematikai leírása úgynevezett reakció-diffúzió differenciálegyenletek felírását és megolását jelenti. Ez így leírva ugyan végtelenül egyszerűnek, sőt unalmasnak tűnik, ha azonban megpróbáljuk megvalósítani, rögtön két nehézséggel is találkozunk.
Először is már az sem nyilvánvaló, hogy hány és milyen egyenletet kell felírnunk, hiszen ehhez részletesen ismernünk kellene a kérdéses folyamat mechanizmusát, vagyis éppen azt, amit felderíteni szándékozunk. A munka tehát mindenképpen legalább részben csupán "próba-szerencse" alapon végezhető.
Aztán ha sikerült megalkotnunk egy olyan modellmechanizmust, amely a kémiával, a fizikával, no meg a saját józan eszünkkel is összegyeztethető, akkor jön a következő kellemetlen meglepetés: a keletkezett egyenletrendszer általában csatolt, nemlineáris egyenletekből áll, amelyeknél a szokásos papír-ceruza-töprengés módszerrel semmire sem megyünk. Ezek az egyenletrendszerek nem oldhatók meg az analitikus matematika eszközeivel, kénytelenek leszünk tehát numerikus eljárásokhoz folyamodni. Az ezekhez szükséges számítási teljesítmény azonban sok esetben akkora, hogy az még a számítástechnika jelenlegi fejlettségi szintjén is problémát jelent..
A Liesegang-jelenség története minderre kiváló példa.

Jellegzetes Liesegang mintázatok: ezüst-kromát gyűrűk zselatinban, illetve két enyhén anomális, lineáris elrendezésű rendszer

Liesegang mintázatok
A Liesegang-jelenség a kémiai mintázatképződések egy speciális formája, amelynél egy rosszul oldódó vegyület elsozlása mutat bizonyos térbeli rendezettséget. Az analitikai kémiából számos olyan reakciót ismerünk, amely csapadékképződéssel, vagyis egy rosszul oldódó anyag keletkezésével jár. Kiváló ppélda erre az ezüst-nitrát (AgNO3) és a kálium-bikromát (K2Cr2O7) reakciója.
Ha e két komponen egyike egy gélben (például zselatinban) van eloszlatva, a másik reaktáns oldata pedig ebbe diffundál bele, akkor a keletkező csapadék a várakozással ellentétben nem egy folytonos zónát fog alkotni a két anyag találkozási pontja körül. Helyette a kísérleti elrendezés geometriájának megfelelően csapadéksávok képződnek, amelyek valamilyen rejtélyes oknál fogva bizonyos egyszerű skálatörvények szerint oszlanak el.
A fenti ábrán egy egy- illetve egy kétdimenziós Liesegang mintázat látható.

Raphael Eduard Liesegang és a periodikus csapadékképződésről megjelent első tudományos közlemény (1896)

A periodikus csapadékképződés történetének hajnala
A név ellenére a periodikus csapadékmintázatok első leírása valójában nem Liesegangtól származik. Frederic Ferdinan Runge már 1855-ben, tehát csaknem fél évszázaddal Liesegang előtt leírt olyan kísérleteket, amelyeknél reakcióközegként szűrőpapírt használt. Ezt nedvesítette meg a csapadékképző reakció egyik reaktánsának oldatával, a másikat pedig rácseppentette. A keletkező mintázatokat Runge "önfestő képeknek" nevezte és egy egész könyvet írt róluk. Ma ez efféle jelenségeket "önszerveződésnek" nevezzük, és gyaníthatólag szakcikkek tízezreit találhatjuk róluk az irodalomban.
Ennek megfelelően talán kissé meglepő, hogy Runge munkásságával túlzottan is megelőzte korát. Kortársai közül gyakorlatilag senki nem vette komolyan, a periodikus csapadékképződés jelensége pedig feledésbe merült egészen 1896-ig. Ebben az évben Raphael Eduard Liesegang, egy német fotográfus és kémikus, aki kálium-dikromát oldatával duzzasztott zselatinlapokkal kísérletezett, az egyik mintadarabra véletlenül ráejtett egy darabka ezüst-nitrát kristályt. Kis idő után meglepődve vette észre, hogy a szemcse körül koncentrikus gyűrűk formájában jött létre az ezüst-kromát csapadék, amelyek kifelé haladva egyre ritkásabban követték egymást. Később kémcsőben is sikerült reprodukálnia a jelenséget.
Liesegang ezt követően részletesen tanulmányozta a véletlenül felfedezett effektust és eredményeiről számos cikket közölt. Tulajdonképpen ennek köszönheti, hogy az utókor kutatói már csak Liesegang-jelenség néven említik a "kváziperiodikus csapadékmintázatok" képződését. (Szokás amúgy Liesegang gyűrűkről, illetve Liesegang sávokról is beszélni.)

Balra: Wilhelm Ostwald, aki az első kvantitatív modellt (tőltelítési modell) javasolta a periodikus csapadékképződés leírására, illetve tőle származik a "Luesegang-jelenség" elnevezés is.
Jobbra: Annak a könyvnek a cínlapja, amelyben Ostwald leírja az említett modellt.
Az első modell
Liesegang megmutatta eredményeit Wilhelm Ostwaldnak, aki nem sokkal ez után, 1897-ben közölte a jelenség első lehetséges magyarázatát általános kémiáról szóló könyvében. Ez volt az úgynevezett túltelítési elmélet, amit később a XX. század során számos szerző próbált finomítani, illetve matematikailag egzakt formába önteni.
Az első néhány évtizedben a Liesegang jelenséggel kapcsolatos irodalom csaknem kizárólag a különféle kísérleti tapasztalatokról szólt. 1923 Jablczinsky észrevette, hogy a csapadéksávok távolságai minden esetben mértani sorozatot alkotnak. Ez a Liesegang mintázatok legalapvetőbb skálatörvénye, az úgynevezett távolságtörvény.
A kísérletes vizsgálatok éveiben rengeteg különféle rendszerben fedeztek fel Liesegang mintázatokat, illetve számos anomliás mintázatképződést is sikerült megfigyelni.

Fejlődés a XX. század során
Bár a XX. század első évtizedeiben számos más, Ostwald modelljétől eltérő magyarázat is napvilágot látott a Liesegang gyűrűkkel kapcsolatban, általában elmondható, hogy a kutatók többsége vagy meg sem próbálkozott matematikailag egzakt modellek fejlesztésével, vagy ha igen, azok gyakorlati értelemben sorra kudarcot vallottak. Ez figyelembe véve a reakció-diffúzió rendszerekkel kapcsolatban korábban említett nehézségeket természetesen nem különösebben meglepő.
A XX. század második felében aztán mind elméleti, mind kísérletes téren történt előrelépés.
A kísérleti módszerek a technika fejlődésének köszönhetően kifinomultabbak, az eredmények pedig pontosabbak és részletesebbek lettek. John Ross, Soichi Kai vagy Stefan C. Müller ebben az időben közölt cikkei például különös részletességgel foglalkoztak a témával, de rajtuk kívül is szerzők ezrei vizsgáltak különféle csapadékmintázatokat. (Egy 1952-ben Kurt H. Stern által készített irodalmi áttekintés már több mint 600 olyan cikket említ, amely kifejezetten a Liesegang-jelenséggel foglalkozik.)

A nagy sebességű számítógépek megjelenése
Az alsó kategóriás, vagy „asztali” számítógépek teljesítménye nagyjából a 90-es évek elején érte el azt a szintet, amely már lehetővé tette reakció-diffúzió rendszerek numerikus megoldását. Ez természetesen új korszakot nyitott a Liesegang-jelenség történetében is. Az első részletes numerikus vizsgálatot Polezhaev és Müller végezte, akik saját modelljüket használták a szimuláció alapjaként. (Ez amúgy az Ostwald által 1897-ben javasolt túltelítési elmélet némiképp kiterjesztett változata volt.)
Ugyanennek a modellnek a továbbfejlesztett változatot vizsgálta Krug és szerzőtársai. Chopard és szerzőtársai egy úhynevezett rács-gáz (lattice-gas) modellt fejlesztettek ki 2D Liesegang mintázatok numerikus reprodukálására. Később ugyanezt a rendszert használta Antal és szerzőtársai az úgynevezett spinodális lebomlási modell (spinodal decomposition) vizsgálatára.
Mindezen erőfeszítések ellenére a Liesegang-jelenségnek a XX. század végéig nem született átfogó magyarázata. Annak ellenére, hogy a jelenség kísérleti oldalról gyakorlatilag teljesen ismertnek tekinthető volt, a vele kapcsolatos irodalom számos olyan effektust és anomáliát tartalmazott, amelynek még csak kvalitatív magyarázata sem létezett.
2003-ig egyetlen olyan modell sem jelent meg az irodalomban, amely akár csak kísérletet tett volna a fordított mintázatok, a spirális alakzatok, a gömbszerű vagy meniszkuszra emlékeztető sávok, a szisztematikusan tovaterjedő hibahelyek, vagy az úgynevezett kettős mintázatok (két, különböző frekvenciájú mintázat egyazon rendszerben) magyarázatára.

Az IDNB modell
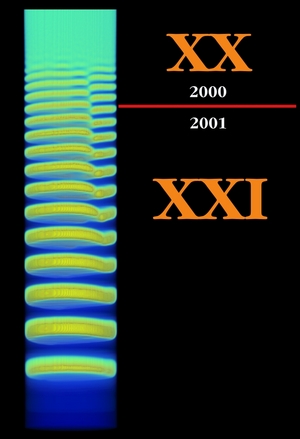
A balra látható kép az IDNB modell egy korai eredménye, amelynek a Liesegang-jelenség szempontjából afféle szimbolikus határkő jellege van. A számítást 2000-ben, szilveszter este indítottam el egy négyprocesszoros klaszteren, aztán mivel egy ekkora rendszer szimulációja akkor még 3,5-4 napig tartott, elmentem a barátainkkal pezsgőzni. Az első négy csapadékzóna tehát még a XX. században „keletkezett”, a többi már a XXI-edikben. Isten hozta Herr Liesegang a tamagocsik, mobiltelefonok és internetre kötött hűtőszekrények korában!
Ebben a pillanatban valójában még én sem ismertem számos részjelenség magyarázatát. Egyes sztochasztikus effektusok már megvoltak, sőt, már a fordított mintázatokat is értettem, a spirális alakzatok képződéséről viszont legfeljebb halvány elképzeléseim voltak.
Az IDNB modell végső formája 2003-ban, a Tisza partján sétálva született meg.